
In other cases, you want to know whether two variables are associated, without necessarily inferring a cause-and-effect relationship. The exercise and pulse data are an example of this, as I determined the speed on the elliptical machine, then measured the effect on pulse rate. In this kind of experiment, you determine the values of the independent variable for example, you decide what dose of the drug each person gets. If you reject the null hypothesis, you would conclude that the amount of drug causes the changes in blood pressure. The null hypothesis would be that there was no relationship between the amount of drug and the blood pressure.
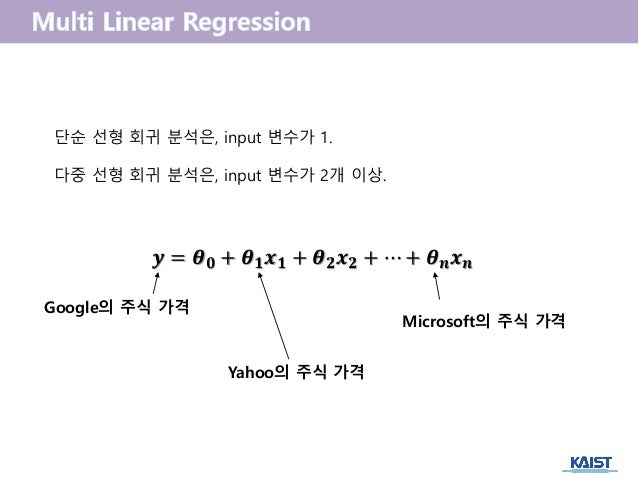
An example would be giving people different amounts of a drug and measuring their blood pressure. In the equation, input values are combined linearly using weights or coefficient values to predict an output value. In some cases, this addresses a biological question about cause-and-effect relationships a significant association means that different values of the independent variable cause different values of the dependent. What Does the Equation Look Like Logistic regression uses an equation as the representation which is very much like the equation for linear regression. You summarize this test of association with the \(P\) value. One is to see whether two measurement variables are associated with each other whether as one variable increases, the other tends to increase (or decrease). There are three main goals for correlation and regression in biology. If the idea of hidden nominal variables in regression confuses you, you can ignore it. I think this rule helps clarify the difference between one-way, two-way, and nested anova. The main value of the hidden nominal variable is that it lets me make the blanket statement that any time you have two or more measurements from a single individual (organism, experimental trial, location, etc.), the identity of that individual is a nominal variable if you only have one measurement from an individual, the individual is not a nominal variable.

For that reason, I'll call it a "hidden" nominal variable.

I'm not aware that anyone else considers this nominal variable to be part of correlation and regression, and it's not something you need to know the value of-you could indicate that a food intake measurement and weight measurement came from the same rat by putting both numbers on the same line, without ever giving the rat a name. There's also one nominal variable that keeps the two measurements together in pairs, such as the name of an individual organism, experimental trial, or location. Use correlation/linear regression when you have two measurement variables, such as food intake and weight, drug dosage and blood pressure, air temperature and metabolic rate, etc. For most purposes, just knowing that bigger amphipods have significantly more eggs (the hypothesis test) would be more interesting than knowing the equation of the line, but it depends on the goals of your experiment.


 0 kommentar(er)
0 kommentar(er)
